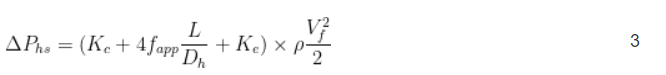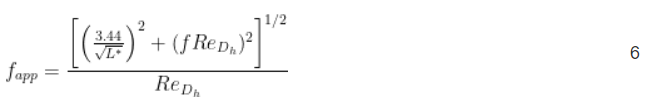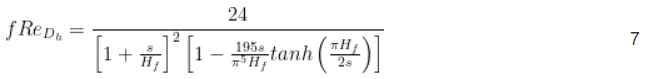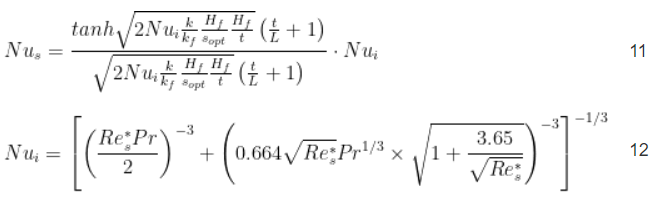El diseño óptimo de los disipadores de calor, especialmente para dispositivos con altas cargas térmicas como MOSFET e IGBT, es fundamental para el funcionamiento eficiente de estos dispositivos y para evitar fallas prematuras de los componentes. Esto requiere una combinación de ventiladores y disipadores de calor para proporcionar una refrigeración adecuada a los dispositivos de alta potencia que disipan grandes cantidades de calor.
Wenxuan Thermal Energy tiene capacidades de personalización profesionales y mercados de aplicaciones diversificados, y puede personalizar productos de refrigeración para diferentes sistemas para los clientes.
Como se muestra en la Figura 1, a menudo se utiliza una cubierta o conducto para dirigir el flujo de aire del ventilador hacia el radiador para evitar el flujo de aire alrededor del radiador, reduciendo así la capacidad de enfriamiento efectiva de la combinación de ventilador y disipador de calor .
Figura 1: Diseño de disipador de calor y ventilador sin bypass
El espaciado óptimo del disipador de calor y la resistencia térmica resultante para la combinación de ventilador/radiador que se muestra en la Figura 1 se pueden calcular directamente usando algunas fórmulas para estimar rápidamente el tamaño del disipador de calor requerido.
Sin embargo, no es factible optimizar el espaciado de las aletas de un disipador de calor suponiendo un caudal constante o un caudal volumétrico. La velocidad del flujo de aire entre las aletas está determinada por el espaciado de las aletas y su número, usando la Ecuación 1. Esta fórmula establece que el flujo volumétrico de aire que se acerca al radiador es el mismo que el flujo volumétrico de aire que pasa a través del radiador porque no hay un flujo de derivación alrededor del radiador.
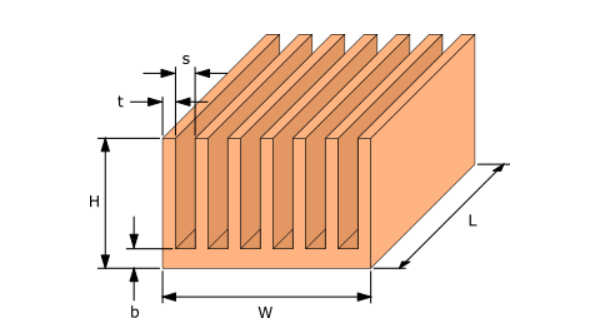
Figura 2: Dimensiones de las aletas de refrigeración por aire
V f :Velocidad del aire entre aletas
V: Flujo volumétrico hacia el radiador
H f =Hb:altura de la aleta
S: espacio entre aletas
N f : número de aletas
Cuanto menor sea la separación de las aletas s , mayor será la velocidad del aire Vf entre las aletas. Cuanto mayor sea el caudal de aire, mejor será el efecto de enfriamiento del disipador de calor. Si desea optimizar el tamaño del disipador de calor, el espacio entre las aletas debe ser un valor pequeño, porque el caudal de aire aumentará a medida que el espacio entre las aletas disminuya y el efecto de enfriamiento también aumentará. En aplicaciones prácticas, el flujo de aire lo proporcionan ventiladores o sopladores. El caudal no es constante y está limitado por el aumento en la caída de presión del disipador de calor a medida que disminuye el espacio s del disipador de calor.
1.Supuestos de diseño del disipador de calor
Para simplificar el análisis y evitar errores de cálculo importantes, haremos las siguientes suposiciones:
a. El área superficial resultante del espesor de la aleta t y del espesor de la base b es mucho menor que el área superficial total del disipador de calor.
b. La fuente de calor tiene el mismo largo y ancho que el disipador de calor y está ubicada en el centro de la base del disipador de calor.
do. La fuente de calor y la base del disipador de calor están en pleno contacto con el ventilador o soplador.
d. Todo el flujo de aire pasa a través del radiador.
mi. En comparación con la convección, la transferencia de calor por radiación es pequeña y puede ignorarse.
F. El flujo de aire a través del radiador es laminar y constante. El espesor del disipador de calor es pequeño en comparación con los espacios entre los disipadores de calor.
Suponer un flujo de aire laminar a través del radiador funciona para la mayoría de las combinaciones comerciales de radiador/ventilador. En electrónica, el ruido del ventilador es una consideración importante, por lo que la velocidad del ventilador se reduce intencionalmente para evitar un ruido significativo al pasar de flujo laminar a turbulento.
2.Calcular el flujo del ventilador
El primer paso en el diseño de un disipador de calor es determinar el punto de funcionamiento de la combinación de ventilador y disipador de calor. Cuando se utiliza un ventilador o soplador con un radiador, el rendimiento del ventilador dependerá del diseño del radiador.
Como se muestra en la Figura 3, cada ventilador tiene una curva de presión/flujo única, donde el caudal es inversamente proporcional a la caída de presión a través del ventilador. Los radiadores también tienen una curva de presión/flujo que es proporcional a la caída de presión a través del radiador, como se muestra en la Figura 3. El flujo a través de la combinación de ventilador/radiador es la intersección de las curvas de presión/flujo del ventilador y del radiador.
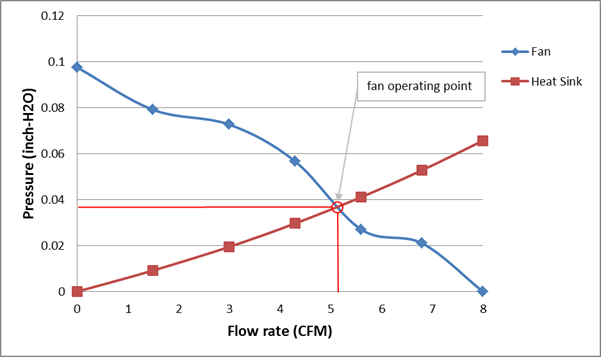
Figura 3: Curvas de presión de ventilador y radiador versus flujo
Las curvas del ventilador generalmente las proporciona el fabricante del ventilador y suelen ser extremadamente no lineales. En muchos casos, los únicos datos sobre el rendimiento del ventilador que proporcionan son el flujo máximo y la caída de presión máxima. Para simplificar los cálculos de flujo y adaptarse a situaciones donde solo se proporcionan el flujo máximo y la caída de presión máxima, se puede expresar una aproximación lineal simple de la curva del ventilador en la Ecuación 2. En la mayoría de los casos, esta aproximación lineal de la curva del ventilador proporciona una estimación razonable de la curva de rendimiento del ventilador.
ΔP max : Caída de presión máxima del ventilador
V máx : flujo volumétrico máximo del ventilador
En el caso de varios ventiladores utilizados uno al lado del otro (en paralelo), el caudal máximo V máx del ventilador es el caudal máximo de un ventilador multiplicado por el número de ventiladores.
La caída de voltaje a través del disipador de calor se muestra en la Ecuación 3:
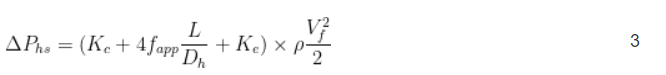
La densidad del aire ρ se calcula a partir de la temperatura del aire ambiente.
El diámetro hidráulico D h del canal entre las aletas se puede aproximar a 2 s . Las variables K c y K e son los coeficientes de pérdida de presión debido a la contracción y expansión del flujo de aire que entra y sale del radiador, respectivamente. Las fórmulas para estos coeficientes de pérdida de presión son función del área frontal σ=s/(s + t) y se basan en el diagrama proporcionado en la Referencia 1.
El coeficiente de fricción aparente fapp se basa en el modelo desarrollado en la referencia [2]:
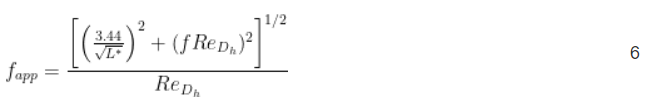
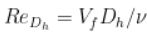, es el número de Reynolds, donde ν es la viscosidad cinemática.
El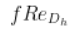 
término de la Ecuación 6 tiene en cuenta el coeficiente de fricción resultante del flujo completamente desarrollado entre las aletas del radiador. El flujo completamente desarrollado ocurre en canales muy largos o en flujos lentos donde el perfil de velocidad del flujo permanece constante.
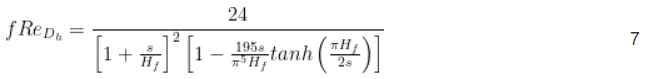
Para determinar el punto de funcionamiento del ventilador/radiador (es decir, la intersección de las curvas de presión/flujo del ventilador y del radiador), se igualan la Ecuación 2 y la Ecuación 3 y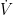 
se determina la variable desconocida.
3.Optimizar el espaciado de las aletas
Calcule el espaciado de aletas S opt que proporciona la máxima transferencia de calor usando la Ecuación 9, donde μ y α son la viscosidad y la difusividad térmica del aire, respectivamente. Esta fórmula fue propuesta por Bejan et al. en ref. 3.
El espaciamiento óptimo de las aletas S opt es una función de la caída de presión del ventilador ΔP y la caída de presión del disipador de calor ΔP hs . La presión de todo el sistema determina la imagen del caudal a través del radiador, y es este caudal el que afecta la tasa de transferencia de calor del radiador.
Sustituya la Ecuación 9 por el espaciado de aletas s en la Ecuación 8 y determine la imagen de flujo del sistema resolviendo la ecuación resultante.
Tenga en cuenta que aunque la Ecuación 8 resuelve ΔP fan y ΔP hs iguales, solo se debe usar la Ecuación 2 ΔP fan cuando se resuelve el flujo en la Ecuación 9. ΔP hs en la Ecuación 3 depende del espaciado de las aletas s , por lo que usar ΔP hs en la Ecuación 9 para resolver el caudal es matemáticamente intratable.
4. Calcular la resistencia térmica del disipador de calor.
A partir de la solución de Ecuación 8, conocemos la imagen del flujo y la velocidad del flujo la Vf a través del disipador de calor, y podemos determinar la tasa de transferencia de calor y la resistencia térmica del disipador de calor.
Calcule el coeficiente promedio de transferencia de calor hf del disipador de calor utilizando las ecuaciones 10, 11, 12, 13 y 14 en la referencia 4.
donde k es la conductividad térmica del aire.
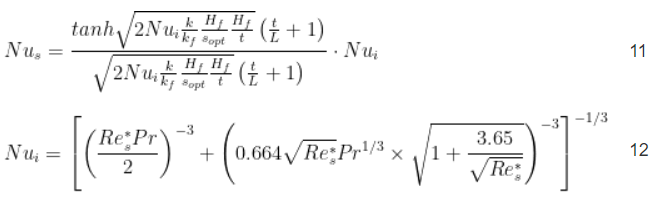
P r es el número de Prandtl del aire; en el rango de temperatura de funcionamiento típico de los disipadores de calor utilizados en refrigeración electrónica se puede utilizar un valor de 0,71.
Por tanto, la resistencia térmica total R hs del disipador de calor es:
El área de superficie mojada de un radiador, A hs , es el área en contacto con el aire que fluye a través del radiador.
El primer término de la Ecuación 15 es la resistencia térmica del disipador de calor y el término después del signo más es la resistencia térmica en la base del disipador de calor.
Para disipadores de calor diversificados , Wenxuan Thermal Energy tiene capacidades de personalización profesionales y mercados de aplicaciones diversificados, y puede personalizar productos de refrigeración para diferentes sistemas para los clientes. Mientras tanto , tendremos en cuenta muchos factores al diseñar el radiador y continuaremos optimizando y mejorando el diseño del radiador. Si tiene alguna otra pregunta sobre los disipadores de calor o necesita una solución de refrigeración adecuada para su negocio, no dude en dejar un comentario o comunicarse con Wenxuan por correo electrónico.
Español
se determina la variable desconocida.
